2010年审计师考试章节辅导讲义：第一章：财务管理基础3

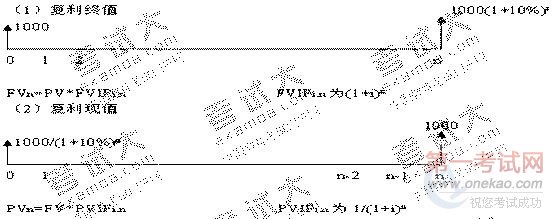
其中，FVn代表复利终值, PV代表复利现值, i代表利率, n代表计息期数, FVIFi,n代表复利终值系数, 1/FVIFi,n代表复利现值系数。

FVn=PV×FVIFi,n

复利终值系数与复利现值系数是一种倒数关系

#

P79【例1-1】【例1-2】

【例题】银行10年期存款年利率为6%，采用复利计息。(1)李某预计10后需要动用一笔10万元资金，现在李某要向银行存入多少现金;(2)王某将2万元现金存入银行，10年后该笔存款的金额是多少。

FVIF6%,10=1.791，1/FVIF6%,10=0.558

#

(1)PV10=10×0.558=5.58万;

(2)FV10=2×1.791=3.582万 #

【例题】(2004)复利终值系数与复利现值系数之间的关系是：( )。

A.二者之和为1 #

B.二者互为倒数

#

C.二者绝对值相等 #

D.二者没有关系

#

【答案】B

3、年金终值和现值(掌握P80)

(1)年金概念与类型：是指相等分期、每期等额的系列收付款项。例如，分期等额赊销收款、分期等额偿还贷款、分期等额支付租金、直线法下的每期等额折旧——年金的终值与现值都是以复利计算的。

#

类型：后付年金(普通年金)、先付年金、延期年金和永久年金

【例题】(2006初)下列各项中，属于年金的有：( )。 #

A.定期支付的固定金额的优先股股利 #

B.每期支付的等额租金 #

C.一次还本付息形式下所偿还的借款利息

#

D.零存整取储蓄中每期存入的等额款项 #

E.每期等额支付的养老金 #

【答案】ABDE #

(2)后付年金

#

涵义：后付年金是指一定时期内每期期末等额收付款项的年金,又称普通年金。

#

①后付年金终值是一定时期内每期期末等额收付款项的复利终值之和。 #

FVAn=A×FVIFA i,n #

②后付年金现值是一定时期内每期期末等额收付款项的复利现值之和。

#

PVAn=A×PVIFA i,n

#

　  #

P81【例1-3】【例1-4】 #

(3)先付年金 #

涵义：先付年金是指一定时期内每期期初等额收付款项的年金,又称即付年金。 #

①先付年金终值是一定时期内每期期初等额收付款项的复利终值之和。 #

Vn=A×(FVIFA i,n+1-1) #

②先付年金现值是一定时期内每期期初等额收付款项的复利现值之和。 #

V0=A×(PVIFA i,n-1+1)

#

P81【例1-5】【例1-6】 #

【例题】(2005、2008初)一定时期内每期期初等额收付的现金是：( )。

A.预付年金 #

B.永续年金 #

C.后付年金 #

D.普通年金

#

【答案】A

#

(4)延期年金现值

#

涵义：在最初若干期没有收付款项的情况下，后面若干期等额的系列收付款项。

延期年金现值计算： #

第一种：假设最初有m期没有年金，后n期有年金。延期年金的现值即为后n期年金贴现至m期第一期期初的现值。 #

计算公式为： V0=A•PVIFAi,n•PVIFi,m

#

其中：A为年金;PVIFAi,n为年金现值系数或年金折现系数;PVIFi,m代表复利现值系数 #

第二种：m+n期都有年金

先求出m+n期后付年金现值，减去没有付款的前m期后付年金现值，二者之差便是延期m期的n期后付年金现值。

#

计算公式为：V0=A•PVIFAi,m+n-A•PVIFAi,m=A•(PVIFAi,m+n-PVIFAi,m)

其中：A为年金;PVIFAi,m+n为m+n年金现值系数或年金折现系数;PVIFAi,m代表年金现值系数 #

P83【例1-7】 #

【例题】某企业向银行借入一笔款项，银行贷款的年利息率为8%，银行规定前10年不用还本付息，但从第11年至第20年每年年末偿还本息1000元，问这笔款项的现值应为多少?

V0=1000•PVIFA8%,10•PVIF8%,10=1000×6.710×0.463=3108(元)

或：V0=1000•(PVIFA8%,20-PVIFA8%,10)=1000×(9.818-6.710)=3108(元)

#

(5)永久年金现值 #

涵义：永久年金是指无限期支付的年金。

计算公式为：V0=A÷i 其中A为年金;i为折现率 #

【例题】某永久年金每年年底的收入为800元，折现率为8%，求该项永久年金的现值。

V0=800÷8% =10000(元) #

(二)货币时间价值的复杂情况(掌握P84)

1、不等额系列现金流量情况与计算原理 #

不等额系列现金流量表现为一定时期内每期现金流量的金额是各不相等的。

计算原理：运用复利终值与现值的原理进行计算，其终值等于各期现金流t期的终值之和，其现值等于各期现金流t期的现值之和。 #

P84【例题1-9】

2、分段年金现金流量情况与计算原理 #

在实务中，同种现金流量在一个时期表现为一种年金;而在另一个时期又表现为另一种年金。这种情况称为分段年金现金流量， #

计算原理：运用年金终值与现值的原理计算。 #

P85【例题1-10】

#

3、年金和不等额系列现金流量混合情况与计算原理

在实务中，年金和不等额系列现金流量相互混合也是常见的情况。这种混合情况有各种表现。 #

计算原理：综合运用复利终值与现值和年金终值与现值的原理。

#

P86【例题1-11】

(三)货币时间价值的特殊情况的计算与运用 #

1、复利计息频数的影响(P87)

复利计息频数(或复利折现系数，下同)是指一年中复利计息(或折现.下同)的频率次数。

计息期数和计息率均可按下列公式进行换算：r=i/m t= n╳m #

公式中，r为期利率，i为年利率，m为每年的计息次数，n为年数，t为换算后的计息期数。

P87【例题1-12】：存入银行1000元，年利率为12%，计算按年、半年、季、月的复利终值。 #

1、按年复利的终值

#

F1=1000×(1+12%)=1120(元) #

2、按半年复利的终值

#

F2=1000×[1+(12%/2)]2=1123.6(元)

3、按季复利的终值

#

F3=1000×[1+(12%/4)]4=1125.51(元) #

4、按月复利的终值

F4=1000×[1+(12%/12)]12=1126.83(元) #

从以上计算可以看出，按年复利终值为1120元，按半年复利终值为1123.6元，按季复利终值为1125.51元，按月复利终值为1126.83元。

#

结论：一年中计息次数越多，其终值就越大。一年中计息次数越多，其现值越小。

2、折现率和折现期的计算(P88)

在实际中会遇到已知终值和现值以及折现期或者折现率，求解折现率或者折现期的要求。

折现率=PVIFi,n=1/FVIFi,n 利用折现率和已知的折现期可以求解项目的投资报酬率，利用折现率和已知的利率可以求解折现期

P88【例题1-14】和【例题1-15】

#